Ever since I got introduced to the joys of Minesweeper by Girl_DM_ I’ve been having a lot of fun playing it as a little timewaster. I’m specifically playing the version from Simon Tatham’s lovely Portable Puzzle Collection (more specifically the Android port via F-Droid) which unlike the original Minesweeper does NOT require guessing. Most of the time, I’m well-versed enough in patterns and testing candidate solutions that I’m able to clear a 16x16 board with 99 mines in about 3-5 minutes. But on a fairly regular basis I’ll run into situations where I get stuck and it seems like I’d either have to calculate an inordinate amount of possible solutions or just make a random guess, neither of which are appealing. Here’s one such example:
with annotations
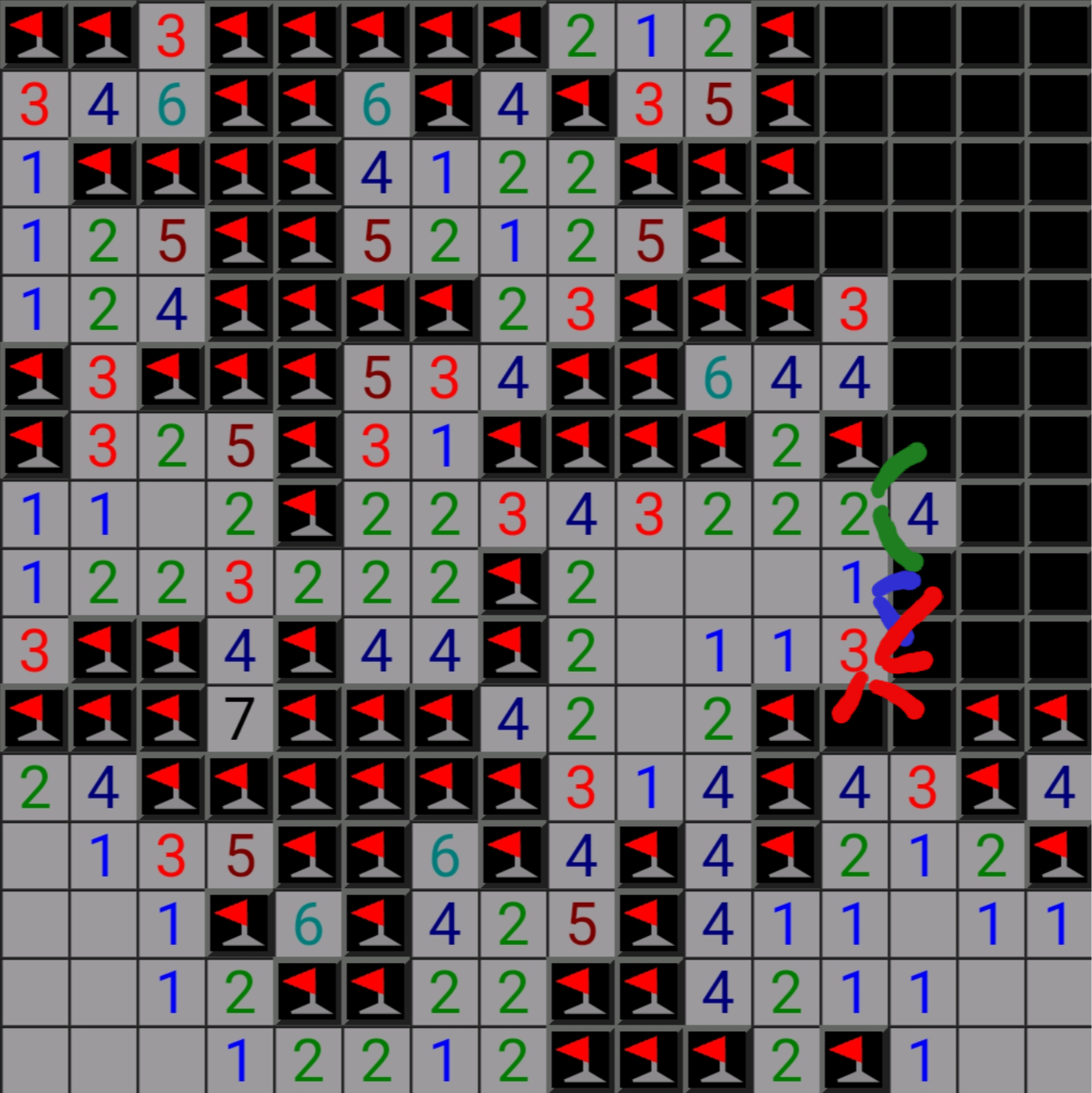
without annotations

There’s probably some cool Minesweeper shorthand I could use to describe the constraints, but what I tried to show with my annotations is how I understand that, for each of the annotated squares, there is a mutually-exclusive binary choice (or in the case of the 3, two choices) for where a mine could be located. Unfortunately, as far as I can tell, while the choices are internally mutually exclusive, it doesn’t seem like there’s any permutation of those choices that is invalid so I can’t eliminate any possibilities. My usual strategy is to fix one choice and see if it results in a contradiction. For instance, if the other mine for the 2 is the upper choice, we can clear the lower square. That means the lower square for the 1 must be a mine, and this still leaves either of the two bottom choices as valid for the 3 (so this is a possible configuration based on these constraints).
The only remaining sections have a lot of freedom which makes them daunting to analyze. Of the remaining unanalyzed squares, from top to bottom they have 2, 2, and 3 mines remaining, respectively, which is quite a lot of options to fully check, and I can only eliminate a few heuristically (e.g. the top 3 must have at least one mine in either the east or southeast space, since otherwise the 4 to the south can’t be fulfilled; the 4 must not have the remaining mines all in the east column because otherwise the 2 and 1 can’t be fulfilled). I’m sure if I went through them methodically I would eventually arrive at an answer, but that’s pretty tedious, so I usually just give up and generate a new board in this kind of situation.
TL;DR: am I missing some neat heuristic(s) that will allow me to either slash the possible solutions to a more manageable number or eliminate individual solutions very quickly, or is this kind of difficult spot just an inevitable outcome for some boards?


You can clear the cell marked with the X since the 1 is satisfied by the flag below it.
…well that’s embarrassing
Thank you though! If you don’t mind, I’ve got a few more for you. First one’s another one where I felt stuck (9 mines remaining, if that helps), second is more just a little overwhelming and I couldn’t figure out a good place to start:
I actually didn’t realize it until looking over the two screenshots, but they both have a pattern that I dread: a T-shaped clearing surrounded by unflagged spaces. Outside of a few specific scenarios with easy solutions (e.g. 5 at the top) it’s something I struggle with a lot, and I wonder if there are any specific heuristics that help in dealing with them beyond “clear stuff nearby until you no longer have a T.”
edit: just figured out the first one (southwest of upper 3 can’t have a mine otherwise the upper 3 can’t be fulfilled) which allowed me to solve the rest in like 20 seconds:
but would still love some pointers for the second one!